Introduction to Whole Numbers
Whole numbers are numbers that start from zero and go on forever without any fractions or decimal parts. In simpler terms, they’re the numbers we can count on our fingers without needing to break them into smaller parts.
Understanding Whole Numbers
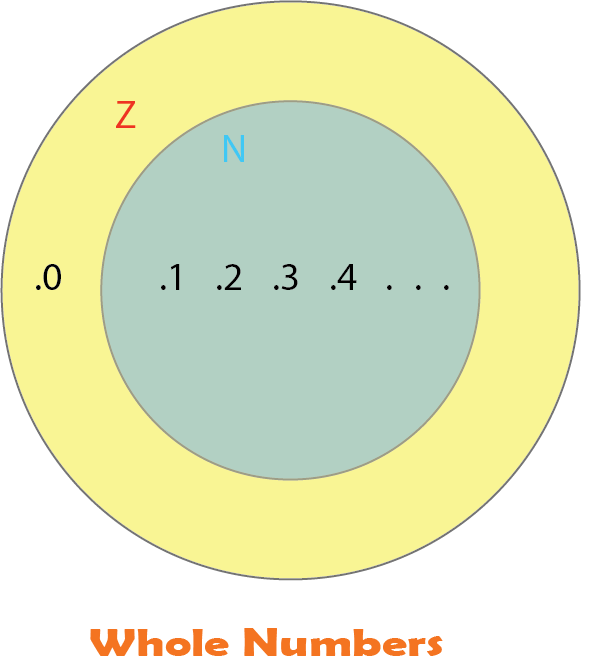
Whole numbers are the numbers that start from zero and extend infinitely without any fractions or decimal parts. They are represented by the symbols 0, 1, 2, 3, … We will discuss the importance of zero as a placeholder and how it distinguishes whole numbers from other types of numbers
Whole Numbers Definition
Whole numbers are all the Natural Numbers (positive integers) along with zero. They are called “whole” because they represent complete units without fractions. The set of Whole Numbers is denoted by Z
Thus Z = {0, 1,2,3,4,5,6,…}
Z comes from the German word “Zahlen” Which means to count.
Note:
- The smallest whole number is zero.
- There is no largest whole number.
- The set of whole numbers is infinite. (unlimited elements)
- Every natural number is a whole number but the converse is not true. i.e(Every whole number is not a natural number)
Role of Zero
Zero is a unique whole number. It represents the absence of quantity or nothingness. It serves as a placeholder in the decimal system, allowing us to represent larger numbers efficiently. Additionally, zero is the additive identity, meaning that when added to any number, it does not change the value of that number.
For example, 5 + 0 = 5. or 39 + 0 = 39 etc.
Whole Numbers on a number line
Whole numbers can be represented on a number line in a similar way to natural numbers. Whole numbers include all the positive integers {1, 2, 3, …} as well as zero (0)
- Zero (0) is usually placed at the center of the number line.
- Positive whole numbers are placed to the right of zero, with each successive number appearing one unit further along the line.
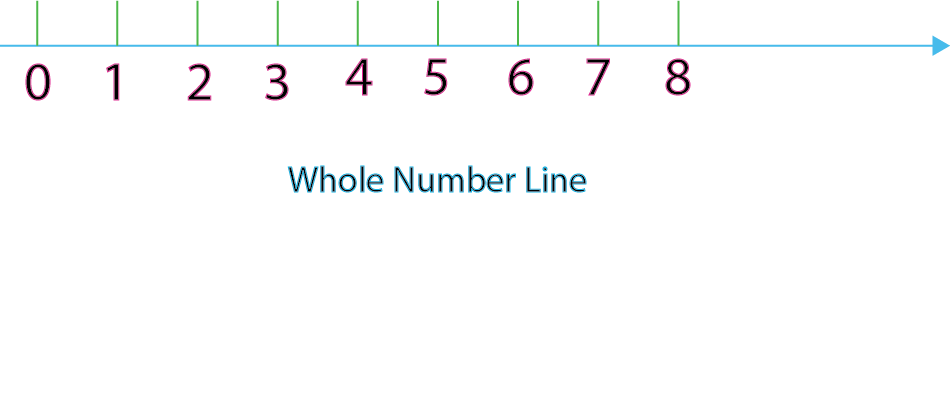
Properties of Whole Numbers
Closure Property
1.The sum or product of any two whole numbers is always a whole number.
Example:
The sum of 3 and 5 (3 + 5 = 8) is a whole number.
Product (3 × 5 = 15), which is also a whole number.
Commutative Property
Whole Numbers are commutative over addition and multiplication. This means that changing the order of the numbers being added or multiplied does not change the result.
For example, 3 + 5 = 5 + 3, and 3 × 5 = 5 × 3.
Associative Property
The addition and multiplication of whole numbers are associative operations. This means that when adding or multiplying three or more numbers, the grouping of the numbers does not affect the result.
For example, (2 + 3) + 4 = 2 + (3 + 4), and (2 × 3) × 4 = 2 × (3 × 4).
Identity Property
The identity element for addition in whole numbers is 0, meaning that adding 0 to any whole number leaves the number unchanged.
For example, 5 + 0 = 5 or 9+ 0 = 9 etc.
The identity element for multiplication is 1, meaning that multiplying any whole number by 1 leaves the number unchanged.
For example, 5 × 1 = 5 or 28 × 1 = 28 etc.
Distributive Property
The distributive property states that multiplication distributes over addition in whole numbers. In other words, when multiplying a number by the sum of two other numbers, is the same as multiplying the number by each of the other two numbers separately and then adding the results. For example, 2 × (3 + 4) = (2 × 3) + (2 × 4).
Applications of Whole Numbers
Here are some simple applications :
Counting
Whole numbers are used for counting objects. Whether it’s counting apples, toys, or people, whole numbers help us quantify and keep track of quantities. For example, if we have 3 apples and someone gives you 2 more, you can count 5 apples in total.
Money
These numbers are used in financial transactions. When dealing with currency, we use whole numbers to represent units of money. For instance, if you have 5 rupees and spend 2 rupees, you’re left with 3
Time
These numbers are used to measure time in hours, minutes, and seconds. For example, if an event starts at 3 o’clock and lasts for 2 hours, it will end at 5 o’clock.
Distance and Measurement
Whole numbers are used to measure distances and quantities. For instance, if we’re measuring the length of a bookshelf, we might find it’s 3 feet long. Or if we have 4 liters of water in a jug and pour out 2 liters, we’re left with 2 liters.
Scores and Grades
Whole numbers are used to represent scores in tests or grades in school. For example, if we score 8 out of 10 on a quiz, our score is represented as the whole number 8.
Quantities in Recipes
Whole numbers are used in cooking and baking to represent quantities of ingredients. For instance, a recipe might call for 2 cups of flour and 3 eggs.
Sports Scores
Whole numbers are used to represent scores in sports games. For example, if a soccer team scores 3 goals and their opponent scores 1 goal, the final score is 3-1.
Number Patterns and Sequences
Number patterns and sequences are arrangements of numbers that follow a certain rule or pattern. Let’s break it down
Number Patterns
A number pattern is a sequence of numbers that follows a specific rule or pattern. This pattern could involve adding, subtracting, multiplying, or consistently dividing the numbers. For example, consider the sequence: 2, 4, 6, 8, 10. In this pattern, each number increases by 2. So, the pattern follows the rule of adding 2 to the previous number to get the next number. So we say that there is common difference 2 in the pattern.
Number Sequences
A number sequence is an ordered arrangement of numbers. Sequences can be finite (having a specific endpoint) or infinite (going on forever). They can also be arithmetic or geometric, among other types.
Arithmetic Sequences
In an arithmetic sequence, each term is found by adding or subtracting the same number from the previous term. For example, consider the sequence: 3, 6, 9, 12, 15. Each term increases by 3. So, this is an arithmetic sequence with a common difference of 3.
Geometric Sequences
In a geometric sequence, each term is found by multiplying or dividing the previous term by the same number. For example, consider the sequence: 2, 6, 18, 54, 162. Here the common ratio is 3, which is a geometric sequence
FAQ
1. What is a Whole Number example?
Whole numbers are the numbers 0, 1, 2, 3, 4, 5, and so on, continuing indefinitely in the positive direction. They have no negative number or fraction.
2. Is 2 a whole number?
Yes, 2 is indeed a whole number. Whole numbers include all non-negative integers.
3. Which is the smallest whole number?
“0” is the smallest number.
4. Which is the largest whole number?
There is no ‘largest’ whole number.
5. What is a whole number in Maths?
In mathematics, a whole number is a type of number that represents a complete quantity or entity without any fractional or decimal parts. Whole numbers are non-negative integers and include all natural numbers (counting numbers) starting from zero.


