Introduction to Irrational Numbers
In mathematics, a number is considered an irrational number if it cannot be expressed as the quotient of two integers, with the denominator not being zero. Unlike rational numbers , which can be neatly expressed as fractions, irrational numbers refuse to conform to such simplicity.
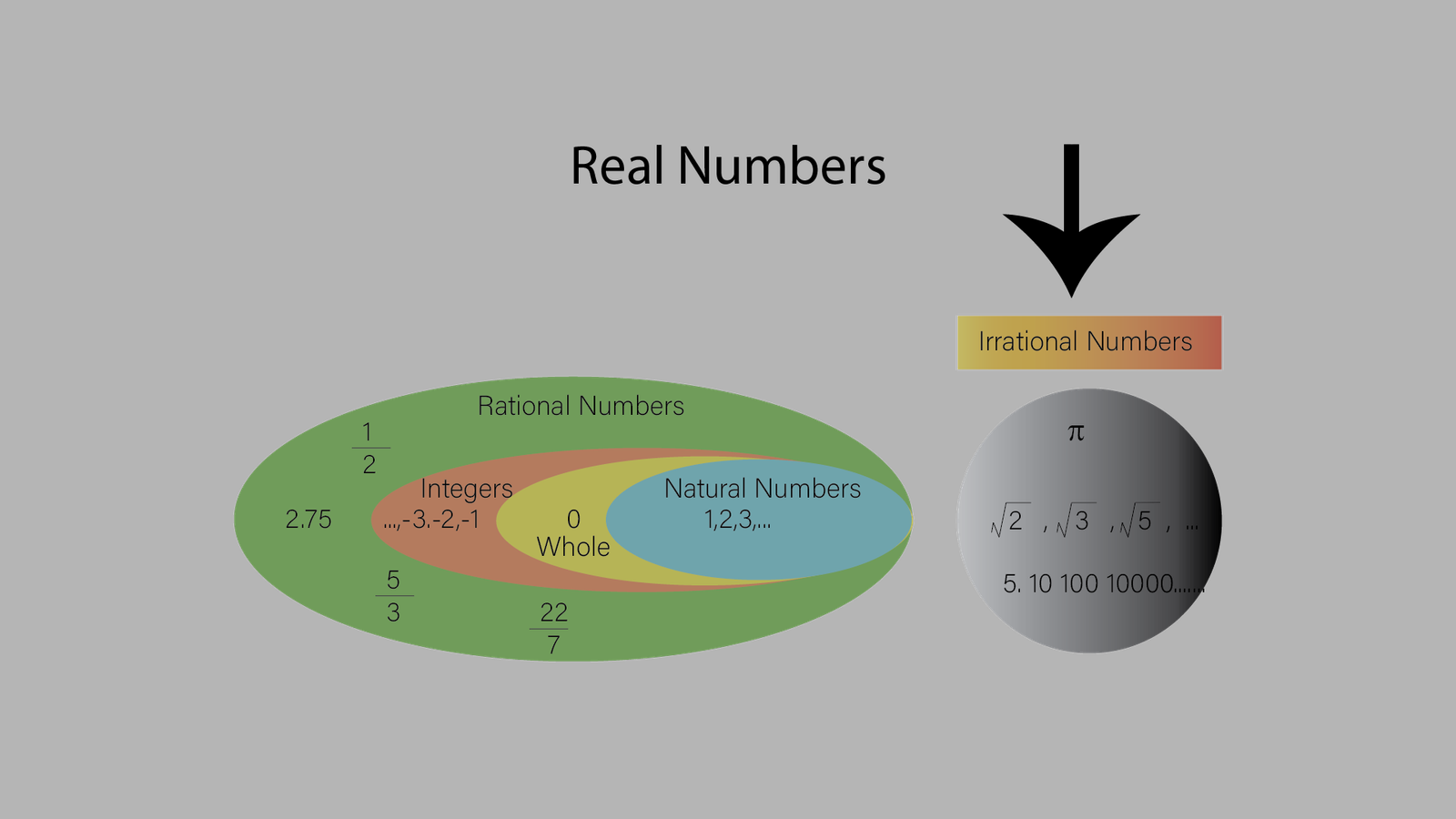
Definition of Irrational Numbers
Irrational numbers are numbers that cannot be expressed as a simple fraction or ratio of two integers (whole numbers), where the denominator (bottom number) is not zero. They are numbers that have non-repeating, non-terminating decimal expansions. Examples of irrational numbers include π (pi), √2 (the square root of 2), and √3 (the square root of 3). These numbers extend infinitely without any predictable pattern, making them a bit unpredictable and “irrational” in nature.
Number Line of Irrational Numbers
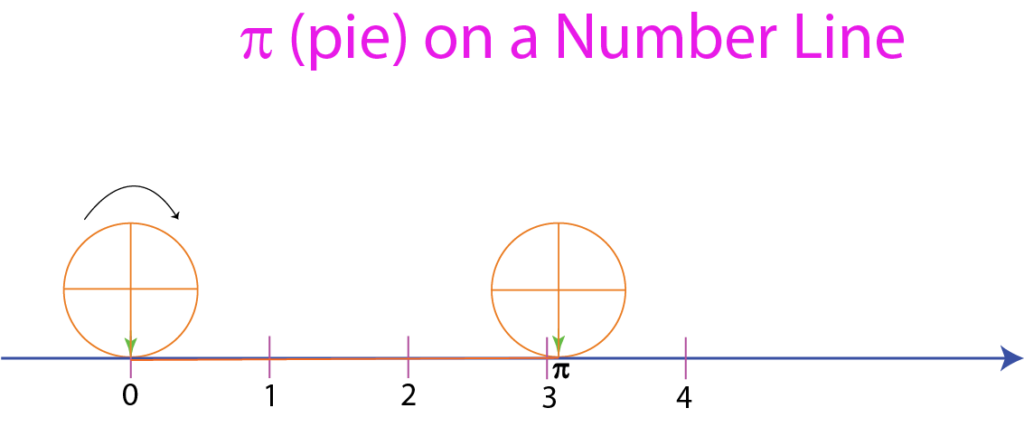
Representing irrational numbers on a number line involves approximating their positions. Since such numbers cannot be expressed as simple fractions, they are located on the number line based on their decimal expansions.
Understand the basics: We know that these numbers are those that cannot be expressed as a fraction of two integers and have non-repeating, non-terminating decimal expansions.—examples: √2, √3, √5,π (pi), etc.
Identify a scale: Decide on a scale for your number line. For example, you might choose to label every integer or every tenth or hundredth.
Locate rational bounds: Find rational numbers (numbers that can be expressed as fractions) that are close to the irrational number we want to represent. For example, if we want to represent √2, you might use 1 and 2 as bounds.
Estimate the position: Using the scale we’ve chosen, estimate where the irrational number falls between the rational bounds. For example, if we’re representing √2 between 1 and 2, we might estimate it’s slightly closer to 1.5 than 2.
Mark the position: Make a small mark on the number line to represent the estimated position of the irrational number.
Optional precision: If you need greater precision, you can calculate more digits of the irrational number to refine its position on the number line. However, remember that irrational numbers have infinitely many non-repeating digits, so we’ll never be able to represent them exactly.
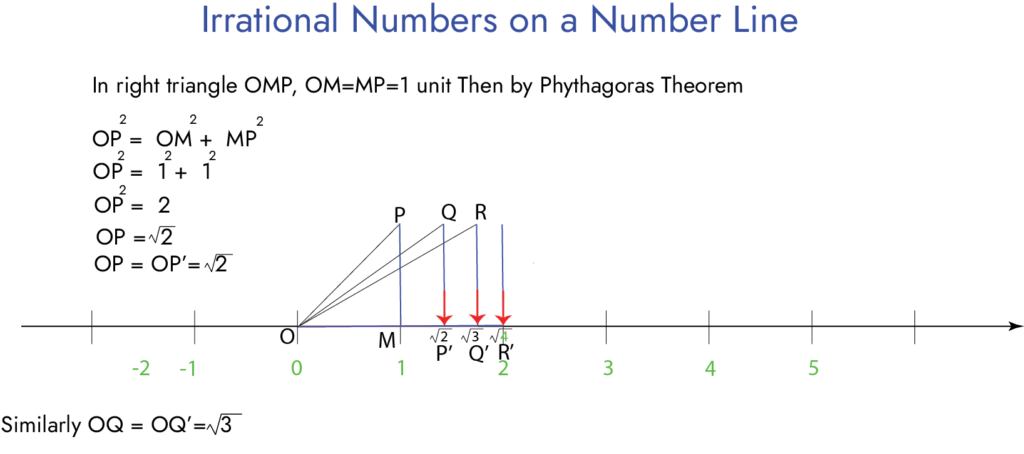
For example, to represent √2 on a number line:
- Choose a scale, let’s say every integer.
- Locate rational bounds: √2 is between 1 and 2.
- Estimate the position: Since √2 is approximately 1.414, it’s closer to 1 than 2.
- Mark the position: Make a mark slightly to the right of 1 on the number line.
Repeat this process for other numbers you want to represent as shown in the following figure.

Representing Irrational Numbers by Phythagoras Theorem
In mathematics, a number is considered irrational if it cannot be expressed as the quotient of two integers, with the denominator not being zero. Unlike rational numbers, which can be neatly expressed as fractions, irrational numbers refuse to conform to such simplicity.
Let's Summarize Irrational Numbers
Definition: Irrational numbers are real numbers that cannot be written as simple fractions. They go on forever without repeating.
Examples: Think of numbers like the square root of 2 (√2) or π (pi). They can’t be expressed as fractions and their decimal representations go on forever without repeating.
Non-repeating, Non-terminating Decimals: Unlike rational numbers (which can be expressed as fractions and have repeating or terminating decimals), irrational numbers don’t repeat or terminate.
- Not Rational: They’re called “irrational” because they’re not rational numbers. Rational numbers can be written as p/q form where q is not equal to 0 and p.q belong to integers.
- Representation on the Number Line: Irrational numbers can be located on the number line just like rational numbers. However, unlike rational numbers which fall at specific points or intervals,
FAQ
Example: √2 , π (pie), 2√3 , 5.1010010000100000000…… , √7
No, π (pie) is not a rational but it is an irrational number because it can’t be expressed in the form of p/q
No π is not equal to 22/7.because it is only its approximate value given as a rational number.
One of the difference between rational and irrational number is that rational numbers are either terminating or non terminating reccuring but irrational numbers are non-terminating and non recurring.
Yes, there are infinitely many irrational numbers between any two distinct rational numbers.


